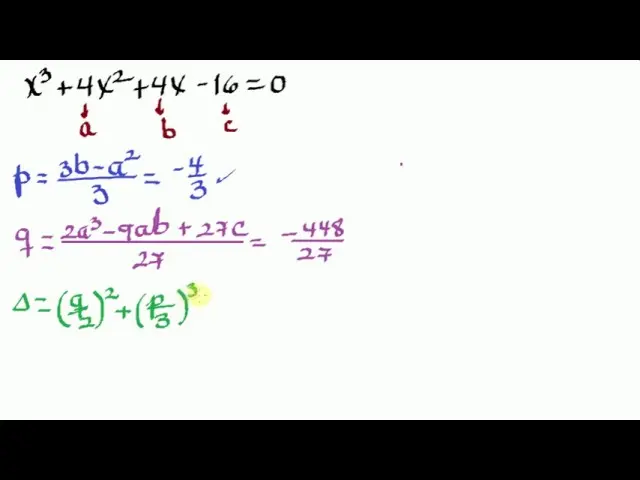Las ecuaciones cúbicas son polinomios de grado tres que pueden tener una o varias soluciones reales o complejas. En el siglo XVI, el matemático italiano Gerolamo Cardano y su discípulo Ludovico Ferrari desarrollaron un método para resolver este tipo de ecuaciones. En este artículo, exploraremos cómo se resuelve una ecuación cúbica utilizando el método de Ferrari y Cardano.
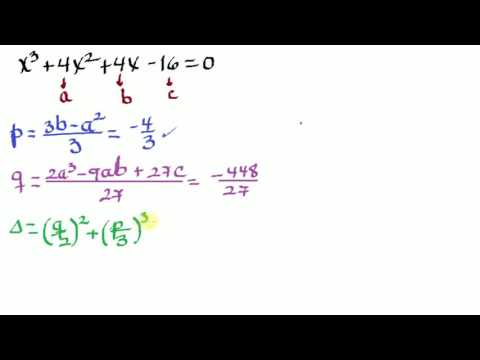
Introducción al método de Ferrari y Cardano
El método de Ferrari y Cardano se basa en la idea de encontrar una raíz conocida de la ecuación cúbica y luego utilizarla para reducir la ecuación a una ecuación cuadrática que pueda resolverse más fácilmente. A través de una serie de pasos, es posible encontrar todas las soluciones reales o complejas de la ecuación cúbica.
Paso 1: Expresar la ecuación cúbica en forma canónica
La primera etapa consiste en expresar la ecuación cúbica en forma canónica, es decir, ponerla en la forma:
ax^3 + bx^2 + cx + d = 0
donde a, b, c y d son coeficientes reales o complejos.
Paso 2: Encontrar una raíz conocida
El siguiente paso es encontrar una raíz conocida de la ecuación cúbica. Esto se puede hacer utilizando diferentes métodos, como la inspección o la aplicación del teorema del factor. Una vez que se encuentra una raíz conocida, digamos r, se puede utilizar la división sintética para dividir la ecuación cúbica por (x-r). El resultado será una ecuación cuadrática.
Paso 3: Resolver la ecuación cuadrática resultante
Después de dividir la ecuación cúbica por (x-r), obtenemos una ecuación cuadrática de la forma:
ax^2 + bx + c = 0
Esta ecuación cuadrática puede resolverse utilizando varios métodos, como la factorización, la fórmula general o completando el cuadrado. Al resolver la ecuación cuadrática, obtendremos dos soluciones, digamos x1 y x
Paso 4: Encontrar las soluciones restantes
Una vez que se han encontrado las soluciones x1 y x2 de la ecuación cuadrática, podemos encontrar las soluciones restantes de la ecuación cúbica utilizando la fórmula de Ferrari. Esta fórmula se basa en la relación entre las raíces de la ecuación cuadrática y las soluciones de la ecuación cúbica.

La fórmula de Ferrari es:
x = (x1 + ∛(q))/(3a) + (x2 + ∛(q))/(3a) - b/3a
donde a, b y q son los coeficientes de la ecuación cuadrática.
Pasos resumidos para resolver una ecuación cúbica
- Expresar la ecuación cúbica en forma canónica.
- Encontrar una raíz conocida y dividir la ecuación cúbica por (x-r).
- Resolver la ecuación cuadrática resultante para obtener x1 y x
- Usar la fórmula de Ferrari para encontrar las soluciones restantes.
Consultas habituales
¿Cuántas soluciones tiene una ecuación cúbica?
Una ecuación cúbica puede tener una, dos o tres soluciones reales o complejas. El número de soluciones depende de los coeficientes de la ecuación y puede determinarse utilizando el método de Ferrari y Cardano.
¿Cuál es la fórmula de Ferrari?
La fórmula de Ferrari se utiliza para encontrar las soluciones restantes de una ecuación cúbica después de haber resuelto la ecuación cuadrática resultante. Esta fórmula se basa en la relación entre las raíces de la ecuación cuadrática y las soluciones de la ecuación cúbica.
¿Cuál es la importancia del método de Ferrari y Cardano?
El método de Ferrari y Cardano es importante en el campo de las matemáticas porque proporciona una forma sistemática de resolver ecuaciones cúbicas. Antes del desarrollo de este método, la resolución de ecuaciones cúbicas era un problema desafiante y no se conocían métodos generales para su solución.
El método de Ferrari y Cardano es una herramienta poderosa para resolver ecuaciones cúbicas. A través de una serie de pasos, es posible encontrar todas las soluciones reales o complejas de una ecuación cúbica. Este método ha sido fundamental en el desarrollo de la teoría de ecuaciones y ha abierto el camino para resolver problemas matemáticos más complejos.
Si quieres conocer otros artículos parecidos a Cómo resolver ecuación cúbica con ferrari y cardano puedes visitar la categoría Ferrari.